Home » October 2020

Structural Geology

on October 17, 2020 in Geology

When the sedimentary rock beds are found to have been deposited without interruption the age difference(s) between adjacent beds are negligible (geologically). We refer such contacts formed between layers and within such sequences as conformable depositional contacts. Conformable depositional contacts are usually planar to slightly irregular in form.

Unconformities

An unconformity is a depositional contact between two rocks of measurably different ages.

Where conformable deposition was interrupted, or where erosion during long intervals removed a part of the rock record an unconformity is formed. The unconformity in places will separate young horizontal sedimentary rocks from older, tilted, deformed sedimentary rocks. In other places the young horizontal sedimentary rocks may rest directly on an erosionally carved surface on old granite or schist. Again, the unconformity marks a gap in the rock record. Time is missing.

Unconformities are divided into three major classes: nonconformities, angular unconformities, and disconformities.

Nonconformity: A geological surface that separates younger overlying sedimentary strata from eroded igneous or metamorphic rocks and represents a large gap in the geologic record.

Nonconformity = top of basement rocks

Angular unconformity: An angular unconformity is an unconformity that separates layers above and below that are not parallel. Classical angular unconformities are horizontal depositional surfaces separating relatively young horizontal strata above from older steeply dipping strata below.

Angular unconformity = hiatus, erosion, and tilt

Disconformity: A disconformity is an unconformity separating strata that are parallel to each other. Some disconformities are highly irregular whereas others have no relief and can be difficult to distinguish within a series of parallel strata. Recognition may require complete knowledge of the ages of beds within the sequence of strata that contains the disconformity.

Disconformity = hiatus + erosion

For all three types of unconformity, the surface marking the unconformity itself is parallel to the bedding or layering of the rocks above the unconformity. The bed directly above an unconformity commonly contains a basal conglomerate, normally composed of clasts of the rock directly beneath the unconformity. Basal conglomerates itself declares erosional intervals. The basal conglomerate may range in coarseness from a thin fine granule conglomerate to a thick coarse boulder conglomerate. Surfaces of unconformity may locally possess topographic relief that can be recognized as the product of ancient erosion, perhaps even including the preservation of the cross-section of an old stream channel. Under ideal conditions, fossil soil profiles, called paleosols, are preserved in rocks directly beneath the old erosion surface. These may be baked where overlain by lava flows.

Paraconformity

A paraconformity is a type of unconformity in which strata are parallel; no apparent erosion is discernable and the surface of the unconformity resembles a simple bedding plane. It is also called pseudoconformity or nondepositional unconformity. Short paraconformities are called diastems.

Paraconformity = hiatus ± erosion (no discernable erosion)

Diastem

A relatively short interruption in sedimentation, involving only a brief interval of time, with little or no erosion before deposition is resumed; a depositional break of lesser magnitude than a paraconformity, or a paraconformity of very small time value.

Diastem = short hiatus ± erosion (a minor paraconformity)

Traps

on October 13, 2020 in Geology

NOMENCLATURE OF A TRAP

The highest point of the trap is the crest, or culmination.

The lowest point at which hydrocarbons may be contained in the trap is the spill point; this lies on a horizontal contour, the spill plane.

The vertical distance from crest to spill plane is the closure of the trap.

The zone immediately beneath the petroleum is referred to as the bottom water, and the zone of the reservoir laterally adjacent to the trap as the edge zone.

Fig1: Cross section through a simple anticlinal trap

Within the trap the productive reservoir is termed the pay.

The vertical distance from the top of the reservoir to the petroleum/water contact is termed gross pay.

All of the gross pay does not necessarily consist of productive reservoir, so gross pay is usually differentiated from net pay.

The net pay is the cumulative vertical thickness of a reservoir from which petroleum may be produced. Development of a reservoir necessitates mapping the gross : net pay ratio across the field.

Within the geographic limits of an oil or gas field there may be one or more pools, each with its own fluid contact.

This field contains two pools, with different oil : water contacts (OWC). In the upper pool the net pay is much less than the gross pay because of non-productive shale layers. In the lower pool the net pay is equal to the gross pay.

DISTRIBUTION OF PETROLEUM WITHIN A TRAP

A trap may contain oil, gas, or both. The oil : water contact (OWC) is the deepest level of producible oil. Similarly, the gas : oil contact (GOC) or gas : water contact is the lower limit of producible gas.

Where oil and gas occur together in the same trap, the gas overlies the oil because the gas has a lower density.

Whether a trap contains oil and/or gas depends both on the chemistry and level of maturation of the source rock and on the pressure and temperature of the reservoir itself.

Fields with thick oil columns may show a more subtle gravity variation through the pay zone. Boundaries between oil, gas, and water may be sharp or transitional. Abrupt fluid contacts indicate a permeable reservoir; gradational ones indicate a low permeability with a high capillary pressure. Not only does a gross gravity separation of gas and oil occur within a reservoir, but more subtle chemical variations may also exist.

Tar Mats

Some oil fields have a layer of heavy oil, termed a tar mat, immediately above the bottom water. Tar mats are very important to identify and understand because they impede the flow of water into a reservoir when the petroleum is produced.

Fluid Contacts

Fluid contacts in a trap are generally planar, but are by no means always horizontal. Correct identification of the cause of the tilt is necessary for the efficient production of the field. There are several causes of tilted fluid contacts.

They may occur where a hydrodynamic flow of the bottom waters leads to a displacement of the hydrocarbons from a crestal to a flank position. This displacement can happen with varying degrees of severity.

In some fields the OWC has tilted as a result of production, presumably because of fluid movement initiated by the production of oil from an adjacent field.

An alternative explanation for a sloping fluid contact is that a trap has been tilted after hydrocarbon invasion, and the contact has not moved.

A third possible cause of a tilted OWC may be a change in facies.

SEALS AND CAP ROCKS

For a trap to have integrity it must be overlain by an effective seal. Any rock may act as a seal as long as it is impermeable. Seals will commonly be porous, and may in fact be petroleum saturated, but they must not permit the vertical migration of petroleum from the trap. Shales are the commonest seals, but evaporites are the most effective. Shales are commonly porous, but because of their fine grain size have very high capillary forces that prevent fluid flow.

Shales may selectively trap oil, while permitting the upward migration of gas. Gas chimneys may sometimes be identified on seismic lines either by a velocity pull-down of the reflector on top of the reservoir, and/or by a loss in seismic character in the overlying reflectors. Indeed some petroleum accumulations are sometimes identified because of their gas-induced seismic anomalies.

CLASSIFICATION OF TRAPS

Wavelet

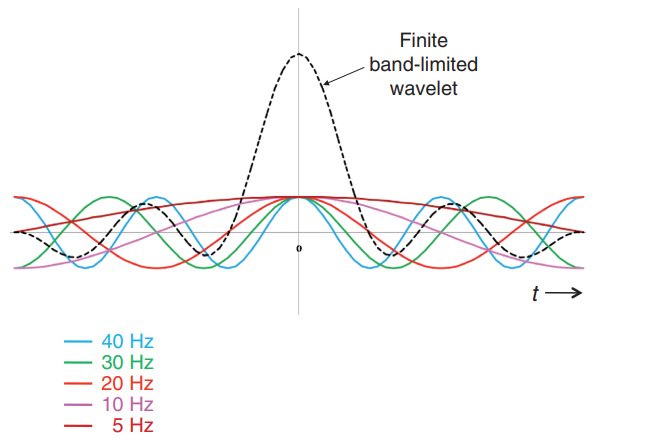
on October 09, 2020 in Signal processing

Practical seismic waveforms are finite and have limited bandwidth. They are the summation of discrete sinusoids, each with its own amplitude, frequency, and phase characteristics.

A band-limited wavelet and its component sinusoids is shown below,

A bandlimited signal cannot be also timelimited. More precisely, a function and its Fourier transform cannot both have finite support unless it is identically zero.

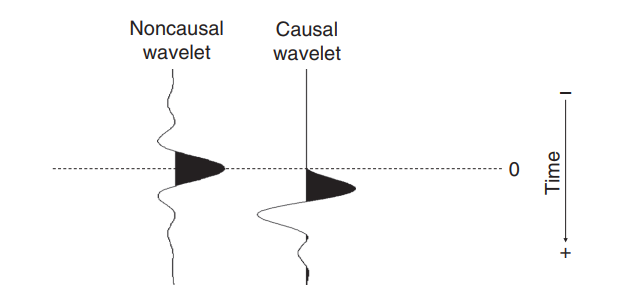
Zero phase

When the wavelet is symmetric about t = 0, it is referred to as a zero-phase wavelet, each of its component sinusoids is zero phase, and each is uniquely defined by its own amplitude and frequency.

Constrained Least Square Inversion

on October 05, 2020 in Inversion

In many geophysical problems it is possible to generate a set of completely different solutions that adequately explain the experimental data, especially where measurement errors are present. Ultimately, one solution has to be selected as the 'best' or most feasible answer to the problem. To do this we have to add to the problem some information not contained in the original equation d=Gm. This extra information is referred to as a priori information and serves to constrain our solutions so as to satisfy any of our quantified expectations of the model parameters. A priori information can take several forms. It may represent previously obtained geophysical, borehole or geological data or may simply be dictated by the physics of the problem. Consequently, constrained inversion takes many forms.

Inversion with prior information

We can incorporate previously obtained information about the sought model parameters in our problem formulation. This external information could be in the form of results from previous experiments or quantified expectations dictated by the physics of the problem. Generally, these external data help to single out unique solution from among all equivalent ones. The solution process is said to be constrained. The procedure is simple. The constraining equations (data) are arranged to form an expression of the form$$Dm=h$$where, D is a matrix (with all the off-diagonal elements equal to zero) that operates on the model parameters m to yield or preserve the the a priori values of m that are contained in the vector h. The equation $Dm = h$ means that we are employing linear equality constraints that are to be satisfied exactly. The mathematical development is straightforward. We wish to bias $m_j$ towards $h_j$.

We simply minimize,

GATE questions Inversion

on October 02, 2020 in GATE questions

GATE 2009

1. Geophysical inverse problems are described by

(a) Fredholm's integral equation of first kind

(b) Fredholm's integral equation of second kind

(d) Legendre equation

2. Spot the ANN method from the following:

(a) Singular value decomposition

(b) monte-car lo technique

(d) Back propagation technique

3. The concept of resolving kernel is used in

(a) Tikhonov's regularization method

(b) Ridge regression method

(d) Simulated annealing method

GATE 2010

1. Unguided random-walk inversion technique signifies

(a) Genetic algorithm

(b) Simulated annealing

(d) Metropolis algorithm

2. If m represents the number of model parameters, d the number of data points and p the rank of matrix to be inverted, then which of the following defines an under determined system?

(a) m < d and p = d

(b) m > d and p = d

(d) m < d and $p \neq d$

GATE 2011

1. The least squares generalized inver se of an overdetermined problem is expressed as

(a) $(GTTG)^{-1}G^T$ (b) $(G^T G)^{-1}$

GATE 2012

1. The solution to the purely under-determined problem Gm = d is given by

(a) $(G^TG)^{-1} G^Td$

(b) $(G^TG)^{-1} Gd^T$

(d) $G^Td(GG^T)^{-1}$

2. Given the following matrix equation: $A_{m\times n} X_{x\times1} = b_{m\times1}$ the nature of this system of equation is

(a) over-determined if m > n

(b) under-determined if m < n

(d) determined by the rank of the matrix A

GATE 2013

1. A singular value of an $m \times n$ matrix, A, is defined as

(a) positive square root of eigenvalue of $AA^T$

(b) modulus of eigenvalue of A

(d) square of eigenvalue of A

2. In an ill-posed geophysical inverse problem, stated as non-singular matrix equation, the magnitude of determinant of the coefficient matrix is

(a) large (b) zero (c) near zero (d) very large

GATE 2014

1. Consider the four systems of algebraic equations (listed in Group I). The systems (Q), (R) and (S) are obtained from (P) by restricting the accuracy of data or coefficients or both respectively, to two decimal places.

Match these systems to their characteristics (listed in Group II)

Group I Group I I

P. x+ 1.0000y = 2.0000 1. instability

x+1.0001y = 2.0001

Q. x+ 1.0000y = 2.00 2. inconsistency

x+1.0001y = 2.00

R. x+ 1.00y = 2.0000 3. non-uniqueness

x+1.00y = 2.0001

S. x+ 1.00y = 2.00 4. exact

x+1.00y = 2.00

(a) P-1; Q-4; R-3; S-2

(b) P-4; Q-1; R-2; S-3

(d) P-1; Q-4; R-2; S-3 50.

2. The eigenvalue (\(Lambda) and eigenvector (U) matrices for singular value decomposition of the matrix

respectively are

GATE 2015

GATE 2016

GATE 2017

GATE 2018

GATE 2019

GATE 2020

Null space

on October 01, 2020 in Inversion

If the seismic velocity in the earth depends only on depth, the velocity can be constructed exactly from the measurement of the arrival time as a function of distance.

Fig1: The traditional definition of the forward and inverse problems

Despite the mathematical elegance of the exact nonlinear inversion schemes, they are of limited applicability. There are a number of reasons for this.

First, the exact inversion techniques are usually only applicable for idealistic situations that may not hold in practice.

Second, the exact inversion techniques often are very unstable.

Third reason is the most fundamental. In many inverse problems the model that one aims to determine is a continuous function of the space variables. This means that the model has infinitely many degrees of freedom. However, in a realistic experiment the amount of data that can be used for the determination of the model is usually finite. A simple count of variables shows that the data cannot carry sufficient information to determine the model uniquely.

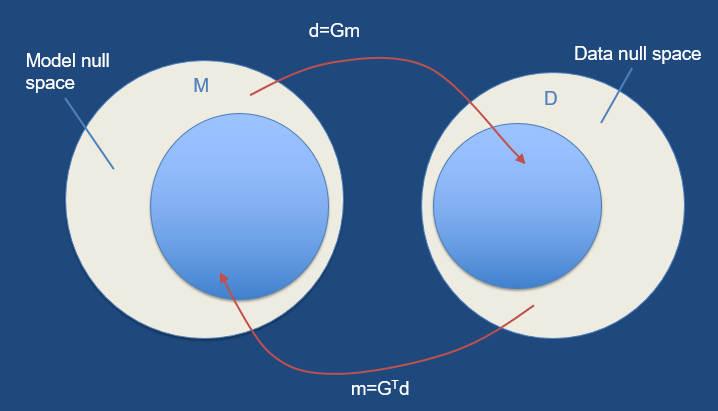
The fact that in realistic experiments a finite amount of data is available to reconstruct a model with infinitely many degrees of freedom necessarily means that the inverse problem is not unique in the sense that there are many models that explain the data equally well. The model obtained from the inversion of the data is therefore not necessarily equal to the true model that one seeks. This implies that the view of inverse problems as shown in fig1 is too simplistic. For realistic problems, inversion really consists of two steps.

Fig2: Inverse problem as a combination of

an estimation problem and an appraisal problem.

Let the true model be denoted by m and the data by d. From the data d one reconstructs an estimated model $m^{est}$, this is called the estimation problem (Fig2). Apart from estimating a model $m^{est}$ that is consistent with the data, one also needs to investigate what relation the estimated model $m^{est}$ bears to the true model m.

In the appraisal problem one determines what properties of the true model are recovered by the estimated model and what errors are attached to it. Thus, $$inversion = estimation + appraisal$$In general there are two reasons why the estimated model differs from the true model. The first reason is the non-uniqueness of the inverse problem that causes several (usually infinitely many) models to fit the data. Technically, this model null-space exits due to inadequate sampling of the model space. The second reason is that real data are always contaminated with errors and the estimated model is therefore affected by these errors as well.

Therefore model appraisal has two aspects, non-uniqueness and error propagation.

Model estimation and model appraisal are fundamentally different for discrete models with a finite number of degrees of freedom and for continuous models with infinitely many degrees of freedom. Also, the problem of model appraisal is only well-solved for linear inverse problems. For this reason the inversion of discrete models and continuous models is treated separately, and the case of linear inversion and nonlinear inversion is also treated independently.

Despite the mathematical elegance of the exact nonlinear inversion schemes, they are of limited applicability. There are a number of reasons for this.

Null space

The vector d of the realisations can be related by a linear function to the vector of model parameters as:$$d=Gm \tag{1}$$where, G is an M x N matrix, and m and b are vectors of dimension N and M respectively. Equation (1) defines G as a linear mapping from an N-dimensional vector space to (generally) an M-dimensional one. But the map might be able to reach only a lesser-dimensional subspace of the full M-dimensional one. That subspace is called the range of G. The dimension of the range is called the rank of G. Sometimes there are nonzero vectors $m_0$ that are mapped to zero by G, that is, $Gm_0=0$. The space of such vectors (a subspace of the N-dimensional space that $m_0$ lives in) is called the nullspace of G, and its dimension is called G’s nullity. The nullity can have any value from zero to N.

System (1) is usually either under- or over-determined, and a least squares solution is sought; unfortunately, we rarely get a unique and reliable solution because it is rank deficient. In fact, the so-called null space exists, constituted by vectors $m_0$ being solution of the associated homogeneous system:$$Gm_0=0\tag{2}$$
Any linear combination of vectors $m_0$ with a solution of (1) still satisfies system (1), and therefore the number of possible solutions is infinite in this case.

Singular value decomposition (SVD) allows to express matrix G by the following product:$$A = USV^T$$where: $U^TU = I$, $V^TV = VV^T = I$ , and I is the identity matrix.

The elements $s_{ij}$ of the diagonal matrix S are the singular values of G. The columns of the matrix V corresponding to null singular values constitute an orthonormal basis of the nullspace, whilst the columns of U corresponding to non-null singular values are an orthonormal base of the range.

Null space Example:

The vector of realizations d can be related by a linear function to the vector of model parameters m as z: $$d=Gm$$ Let us suppose that the inverse problem has two distinct solutions m1 and m2.

So, $$Gm1=d$$
and $$Gm2=d$$
Subtracting these two equations yields
$$G(m1-m2)=0$$
Since, the two solutions are by assumptions distinct, their difference $$m_0=m_1-m_2$$ is non-zero.

The converse is also true, any linear inverse problem that has null vectors then it has non-unique solution. If $m_{par}$ (particular) is an non-null solution to $Gm=d$, for instance minimum length solution, then $m_{par}+\alpha m_0$, is also a solution any choice of $\alpha$.

Note that since $\alpha m_0$ is a null vector for any non-zero $\alpha$, null vectors are only distinct if they are linearly independent.

If a given inverse problem has a q distinct null solutions, then most general solution $$m_{gen}=m_{par}+\sum_{i=1}^{q} \alpha_i m_0$$

The data null space

Linear combinations of data that cannot be predicted by any possible model vector m. For example, no simple linear theory could predict different values for a repeated measurement, but real repeated measurements will usually differ due to measurement error. If there is a data null space, and if the data have a component in this null space, then it will be impossible to fit them exactly.

The model null space

A model null vector is any solution to the homogenous problem $$Gm_{0}=0$$This means we can add in an arbitrary constant times any model null vector and not affect the data misfit. So, the existence of a model null space implies non-uniqueness of any inverse solution.

Both a Model and a Data Null Space

In the case of a data null space, we saw that the generalized inverse solution minimized the least squares mis-fit of data and model response. While in the case of a model null space, the generalized inverse solution minimized the length of the solution itself. If there are both model and data null spaces, then the generalized inverse simultaneously optimizes these goals.

Null space from SVD

Column vectors of U associated with 0 (or very near-zero) singular values are in the data null space.

Column vectors of V associated with 0 singular values are in the model null space.

Minimum length solution never contains any null vectors. But if we use other solution simply(flatness/roughness), those solutions will contain null vectors.

Geo Markdown

Geophysics in short.