GATE 2009
1. Which of the following parameters is uniquely resolved by residual gravity anomaly data
(a) lateral density contrast
(b) excess/deficit mass
(c) absolute density
(d) geometric dimensions of geophysical model
2. The presence of crustal root beneath a mountain chain can be best explained by
(a) Pratt's model (b) Airy's model
(c) Vening Meinesz model (d) Plume model
3. For under water gravity measurements, the following correction is needed:
(a) Prey correction (b) Free-air correction
(c) Bouguer correction (d) Isostatic correction
Common Data for Questions 4 and 5:
The peak gravity anomaly over a 2-D line mass of circular cross-section (horizontal cylinder) of density contrast 500 kg/m3 is 1.674 mGal. The anomaly decreases to 0.837 mGal at a distance of 500 m along a principal profile. The universal gravitation constant, \(G = 6.6667 \times 10^{-11}\ \ m^3sec^{-2}kg^{-1}\).
4. The depth (m) to center of line mass and radius (m) of the horizontal cylinder are =
(a) 500, 199.80
(b) 200, 150.93
(c) 200, 100.33
(d) 100, 60.37 56.
5. Hence compute the excess mass per unit length (kg/m) of the line mass
(a) \(11.0 \times 10^{7}\), (b)\(9.0 \times 10^{7}\)
(c) \(6.27 \times 10^{7}\) (d)\(3.67 \times 10^{7}\)
GATE 2010
1. If the average crustal thickness is 35 km and the height of a mountain is 5 km above mean sea level the crustal thickness based on Airy's model beneath the mountain will he approximately
(a) 35 km (b) 40 km (c) 50 km (d) 70 km
2. The equipotential sur face over which the gravitational field has equal value is known as
(a) geoid (b) spheroid (c) ellipsoid (d) mean sea level
3. Among the following, the best reconnaissance method for determining basement configuration of sedimentary basins is
(a) gravity method (b) self potential method
(c) seismic method (d) electromagnetic method
4. The gravity value measured at the base of a 10 m tall building is 40 mGal. The value at the top of the bullding ignoring its mass is close to
(a) 20 mGal (b) 37 mGal (c) 40 mGal (d) 43 mGal
5. Upward continuation technique filters ________ wavelength anomalies and ____ their amplitudes.
(a) short, reduces (b) long, enhances (c) long, reduces (d) short, enhances
Common Data (or Questions)
The terrain correction in gravity method accounts for topographic relief in the vicinity of the observation point. The Bouguer slab assumes the topography around the observation point to be flat. In the figure below, the Bouguer slab thickness is h and the hollow portion P lies within the Bouguer slab. Q and Rare parts of the topography
(a) half of that in R (b) negative (c) zero (d) positive
7. In the region Q, the terrain correction is required to account for
(a) hollow portion P
(b) reduced gravity due to excess mass in portion Q
(c) increased gravity due t o excess mass in portion Q
(d) over-correction of Bouguer slab
GATE 2011
1. The acceleration due to gravity (g) and universal gravitational constant (G) are related by the expression (Me and Re are the mass and radius of the earth, respectively)
2. Gravity measurement is made on a ship sailing at the speed of 6 knots in the direction N65°E at 20°N latitude. The Eotvos correction (in mGal) is
(a) +38.5 (b) +24.5 (c) – 35.5 (d) – 39.5
Statement for Linked Answer Questions
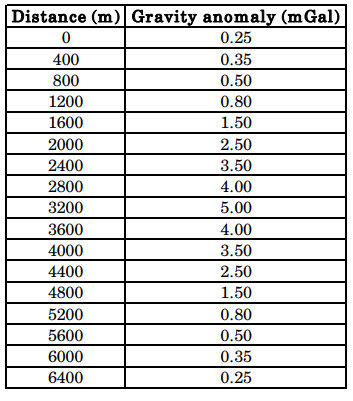
A gravity survey is conducted over a highly compact ore deposit (spherical shape). Bouguer anomaly values reduced along a profile are given below.
3. What is the depth to the center of the ore deposit?
(a) 3100 m (b) 1820 m (c) 1560 m (d) 1450 m
4. What is the excess mass (in metric tons) by the deposit?
(a) 1.615 × 10^8 (b) 2.165 × 10^8 (c) 1.312 × 10^9 (d) 1.825 × 10^9
GATE 2012
1. Bouguer correction is applied to correct for the gravity anomaly due to mass between station location and
(a) mean sea level (b) local datum plane
(c) base of upper crust (d) Mohorovicic discontinuity
2. The change in gravity caused by Earth’s tides on the land surface in a complete tidal cycle is in the range of (in milligal)
(a) 0.1 to 0.2 (b) 0.2 to 0.3 (c) 0.3 to 0.4 (d) 0.4to 0.5
GATE 2013
1. The acceleration due to gravity, 'g' is maximum at
(a) equator (b) poles (c) mid-latitudes (d) sub-tropical regions
2. Which of the following is useful to estimate the depth to the centre of a spherical body from a gravity anomaly curve?
(a) Surface integration (b) low-pass filtering Volume integration (c) Twice the absolute maximum (d) Half-width of the anomaly
3. If L, B, F and T respectively stand for Latitude correction, Bouguer correction, Free-air correction and Terrain correction, then the order in which they will have to be applied for gravity data analysis is
(a) LFBT (b) LBTF (c) FLBT (d) TBLF
GATE 2014
(a) non-rotating homogeneous spherical earth model
(b) decreases rotating inhomogeneous spherical earth model
(c) rotating homogeneous oblate spheroidal earth model
(d) rotating inhomogeneous oblate spheroidal earth model
2. Compute the maximum value of gravity anomaly in µGal over a buried sphere from the following data:
Radius of a sphere = 5 m
Depth to centre of sphere =11 m
Density contrast = 0.1 gm/cc
G = 6.673 × 10– 8 dyne-cm2 /gm2
(a) 2887.58 (b) 288.76 (c) 28.88 (d) 2.89
GATE 2015
1. The shape of the earth is best described as
(a) spheroid (b) prolate ellipsoid (c) ellipsoid (d) oblate spheroid
2. Considering the Airy isostatic compensation for a mountain having elevation of 2.0 km above the mean sea level at a point P, the thickness of its root below P would be _________km. (consider densities of crustal rocks and upper mantle as 2.7 g/cc and 3.3 g/cc respectively).
3. . The Bouguer anomaly obtained after applying all necessary corrections is due to
(a) topographic undulations above the datum
(b) increase in densities of crustal rocks with depth
(c) lateral density variations
(d) vertical density contrast across Moho
GATE 2016
1. According to Airy’s model, gravity anomalies for fully isostatically compensated topography are characterized by
(a) negative Bouguer anomaly and positive free-air anomaly.
(b) positive Bouguer anomaly and negative free-air anomaly.
(c) zero Bouguer anomaly and negative free-air anomaly.
(d) positive Bouguer anomaly and zero free-air anomaly.
2. The value of free-air correction (assuming sea level as datum plane) at an elevation of 150 m is _________ mGal.
3. A spherical cavity of radius 8 m has its centre 15 m below the surface. If the cavity is full of sediments of density \(1.5 \times 10^3 kg/m3\) and is in a rock body of density \(2.4 \times 10^3 kg/m3\), the maximum value of its gravity anomaly is __________ mGal.
4. Match the items (listed in Group I) with the corresponding corrections applied for reduction of marine gravity data (listed in Group II).
(a) P-4; Q-3; R-1; S-2 (b) P-2; Q-3; R-4; S-1 (c) P-4; Q-1; R-2; S-3 (d) P-3; Q-1; R-4; S-2
GATE 2017
1. The normal gravity formula (for e.g. GRS80) is a function of
(a) geocentric latitude (b) geodetic latitude (c) longitude (d) altitude
2. Given the Bouguer density of 2.8 g/cc, the Bouguer correction for a gravity station at an elevation of 30 m above the datum is ____ mGals. (Use \(\pi\) = 3.14)
GATE 2018
1. The geoid can be best defined as
(a) an oblate spheroid that best approximates the shape of the earth.
(b) a surface over which the value of gravity is constant.
(c) the physical surface of the earth.
(d) an equipotential surface of gravity of the earth.
2. Which one of the following corrections is always added during reduction of the observed gravity data?
(a) Latitude (b) Free-air (c) Bouguer (d) Terrain
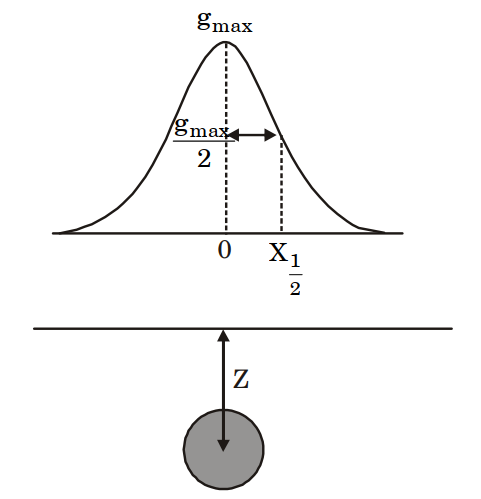
3. In the figure below, Z denotes the depth to the center of a buried sphere from the surface and \(X_{1/2}\) denotes the half-width of the profile at half the maximum value of gravity. Then, the ratio \(\frac{Z}{X_{1/2}}\) is ________.
4. Two survey vessels with shipborne gravimeters are cruising towards each other at a speed of 6 knots each along an east -west course. The difference in gravity readings of the two gravimeters is 63.5 mGal at the point at which the survey vessels cross each other. The latitude along which the survey vessels are cruising is ______ °N.
5. A gravity reading is taken in a stationary helicopter hovering 1 km above mean-sea level at a particular location. The difference in the value of g measured in the helicopter and at mean sea level vertically beneath the helicopter is ____________ mGals.
GATE 2019
1. Which one of the following is only a correction and not a reduction in the computation of gravity anomalies with respect to a datum?
(a) Free air (b) Bouguer (c) Terrain (d) Isostatic
2. Assuming Airy isostatic compensation, the depth to the Moho from a point located 2 km above the mean sea level is _____ km. (round off to 1 decimal place). (The depth of compensation T for the crust at mean sea level is 30 km, the density of crust and upper mantle are 2.67 gm/cc and 3.30 gm/cc, respectively).
3. In gravity anomalies, the ‘Indirect effect’ mainly arises from__________.
(a) the sources outside the area of investigation
(b) improper instrument drift
(c) effect of mass lying between the geoid and ellipsoid
(d) short-wavelength uncompensated masses in the subsurface
4. Which one of the following statements about the gravity anomalies on land is CORRECT?
(a) Free-air and Bouguer anomalies are always positively correlated with elevation
(b) Isostatic anomalies are not useful to understand the crustal heterogeneities
(c) Vertical derivatives are used to enhance the gravity effects of deep-seated bodies
(d) X-horizontal gradient \(dg/dx\) map enhances/sharpens anomalies of bodies trending N-S (X-East, Y-North, Z-downward).
5. In an abandoned mine-site, three hollow spherical cavities are located below the surface centered at depths of 50, 100 and 150 metres. Assuming that residual gravity is low due to each one of these cavities are small (~ 0.05 mGal), do not interfere and can be detected by the gravimeter, the most ideal (largest) grid spacing for carrying out the gravity surveys in order to correctly delineate these cavities is __________ metres, (round off to the nearest integer).
GATE 2020
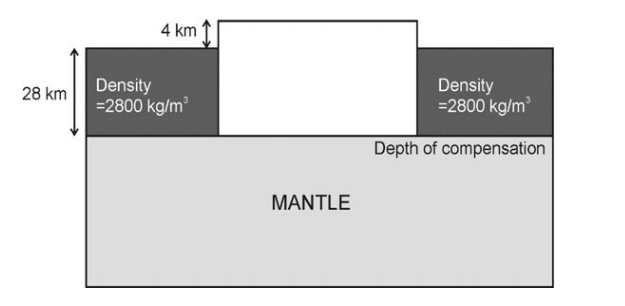
1. A 4 km-high plateau is isostatically compensated as shown in the figure. Assuming Pratt’s hypothesis of isostasy, the calculated density of the plateau is _____ kg/m3.
(a) Non-rotating homogeneous spherical Earth model
(b) Non-rotating homogeneous oblate spheroidal Earth model
(c) Rotating homogeneous oblate spheroidal Earth model
(d) Rotating inhomogeneous spherical Earth model
3. A micro-gravity survey with appropriate station spacing is performed to detect a subsurface spherical cavity in a bedrock of density 2500 kg/m3. The depth to the center of the cavity is 4 m from the surface and the elevation measurement accuracy of the surveying instrument is 0.1 m. The smallest cavity that can be detected by the survey must have a radius greater than _______ m. (Round off to 1 decimal place) (Assume \(G = 6.673 \times 10^{-11} m^3kg^{–1}s^{–2}\)).
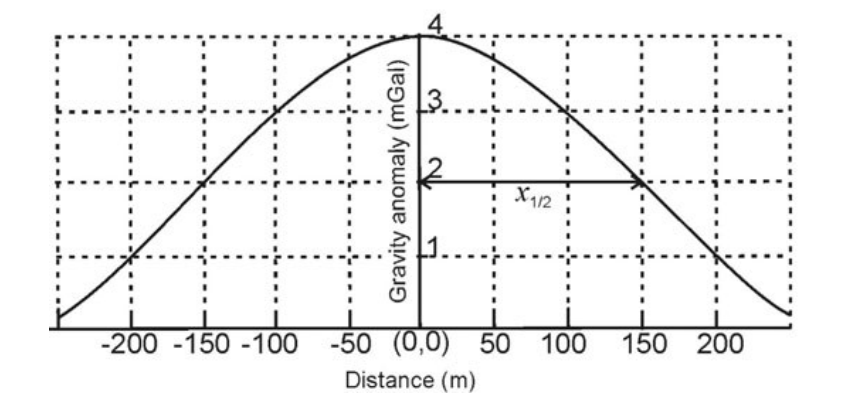
4. The gravity anomaly over a spherical ore body is shown in the figure below. The calculated excess mass due to the ore body will be _______ × 1010 kg. (Round off to 1 decimal place) (Assume \(z = 1.3 \times x_{1/2}\); \(G = 6.673 \times 10^{-11} m^3kg^{–1}s^{–2}\)).