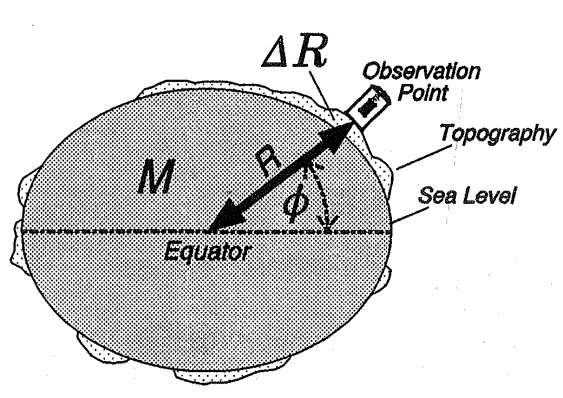
Free Air Gravity Anomaly
Gravity observed at a specific location on Earth's surface can be viewed as a function of three main components:
- the latitude (\(\phi\))of the observation point, accounted for by the theoretical gravity formula;
- the elevation (\(\Delta R\)) of the station, which changes the radius (R) from the observation point to the center of the Earth; and
- the mass distribution (M) in the subsurface, relative to the observation point.
Indirect effect and Cogeoid
When removing the effect of the Bouguer plate and/or the train undulations, we actually disregard the masses above the geoid. In other words, when using the Bouguer anomaly, we mathematically change the real distribution of masses, the potential of the earth and hence even the geoid. This distortion is usually called the indirect effect of mass removal and the surface thus distorted is known as Compensated Geoid or Cogeoid.
Geophysical indirect effect
The indirect reduction or correction, which is applicable to the calculation of all gravity anomalies, is the gravitational effect resulting from the use of different vertical datums for establishing the height and theoretical gravity at a station’s position. It represents the difference between the geoidally obtained gravity measurements and the ellipsoidally referenced mapping system.
The indirect effect combines the gravitational effect of the difference in height between the geoid and ellipsoid at the station and the mass effect of the included material.
Assuming a horizontal layer of thickness equal to the difference in height (the geoidal height or undulation) and a density of 2,670 kg/m3, the effect is $$g_{ind} = (0.3806 − 0.1119)N = 0.1976 \ N $$ where N is the geoidal height in meters and \(g_{ind}\) is the indirect reduction in milligals.
If the geoid is above the ellipsoid, the indirect reduction has the same sign as the elevation correction and vice versa.