Seismometers are instruments that measure and record motions of the ground, including those of seismic waves generated by earthquakes, nuclear explosions, and other seismic sources. Records of seismic waves allow seismologists to map the interior of the Earth, and locate and measure the size of these different sources.
Seismograph is often used to mean seismometer, though it is more applicable to the older instruments in which the measuring and recording of ground motion were combined than to modern systems, in which these functions are separated.
Seismoscopes which merely indicate that motion has occurred and perhaps with some simple measure of how large it was.
The record of earthquake event is called seismogram.
A datalogger (also know as data acquisition system or DAS) is piece of electronic equipment which converts an input into a digital time series representation.
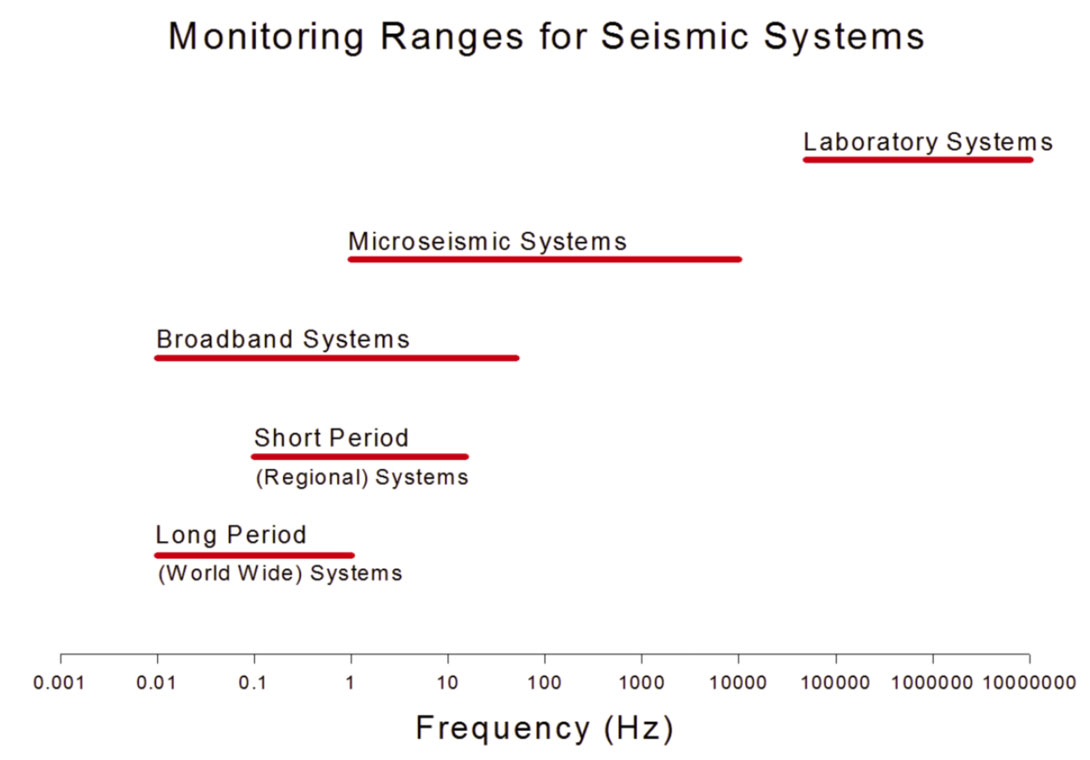
Types of seismometers:
Broadband Sensors - are three-component seismometers capable of sensing ground motions over a wide frequency band. These sensors are most-often used in passive experiments. The flat-to-velocity portion of the bandwidth is generally about 0.01 Hz (100 sec) to 25Hz.
Intermediate Sensors - are three component seismometers with corner periods in the 30- to 40-second range (distinct from the 120- to 240-second range of PASSCAL's truly broadband fleet). These sensors, like their broadband cousins, are capable of sensing ground motions of much longer period than their corner periods, if the long-period amplitudes are sufficient.
Short-Period Sensors - are rugged three-component seismometers that cover higher-frequency bands (usually 1 Hz to 100+ Hz). These sensors are used in both passive and active-source experiments. The sensors, themselves, can be either feedback seismometers requiring power or conventional, passive seismometers requiring no external power.
High-Frequency Sensors - are very rugged seismometers that cover even higher frequency bands (e.g. 4.5 Hz to 100+ Hz). These sensors are most-often used in active-source experiments and are often referred to as geophones.
Accelerometers - also known as strong-motion sensors, are designed to measure the large amplitude, high frequency seismic waves typical of large local earthquakes, and operate in the frequency band 0 Hz to 100+ Hz.
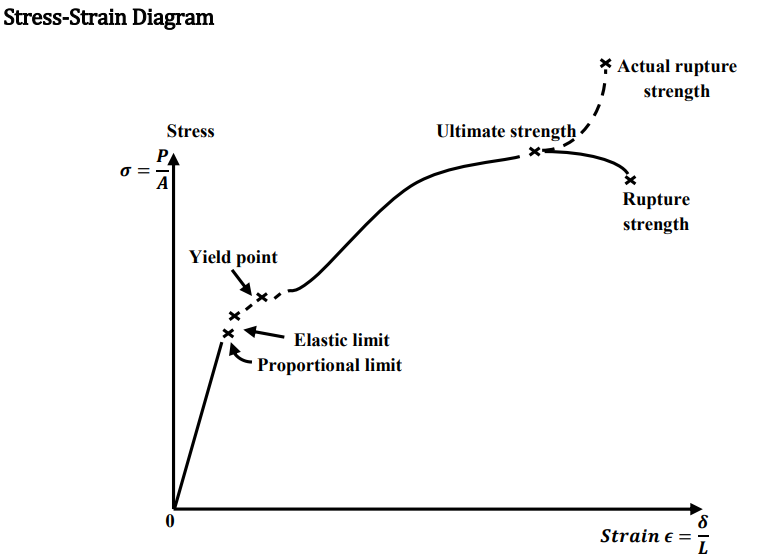
Proportional Limit: It is the point on the stress strain curve up to which stress is proportional to strain.
Elastic Limit: It is the point on the stress strain curve up to which material will return to its original shape when unloaded.
Yield Point: It is the point on the stress strain curve at which there is an appreciable elongation or yielding of the material without any corresponding increase of load; indeed the load actually may decrease while the yielding occurs.
Ultimate Strength: It is the highest ordinate on the stress strain curve.
Rupture Strength: It is the stress at failure
Mohr’s Circle
Mohr's circle gives us a graphic tool by which, we can compare the different stress transformation states of a stress cube to a circle. Each different stress combination is described by a point around the circumference of the circle.
Notes:
- + τ (opposite convension may also be used) (meaning counterclockwise around the cube) is downward
- - τ (meaning clockwise around the cube) is up on the axis
- + σ for tensile stress
- - σ for compressive stress
- A rotation angle of θ on the stress cube shows up as 2θ on the circle diagram and rotates in the same direction.
- The largest and smallest values of σ are the principle stresses, σ1 and σ2.
- The largest shear stress, τmax is equal to the radius of the circle, R.
- The center of the circle is located at the value of the average stress, σave
- If σ1 = σ2 in magnitude and direction (nature) the Mohr circle will reduce into a point and no shear stress will be developed.
- If the plane contain only shear and no normal stress (pure shear), then origin and centre of the circle will coincide and maximum and minimum principal stress equal and opposite. σ1= + τ , σ2 = - τ
- The summation of normal stresses on any two mutually perpendicular planes remains constant. σx + σy = σ1 + σ2